สำหรับการหาปริพันธ์บนช่วงที่ต้องการ หลักการหาก็คือการประมาณโดยการหาพื้นที่ใต้กราฟนั่นเอง โดยสำหรับวิธีการหาพื้นที่ใต้กราฟให้ค่าใกล้เคียงกับค่าปริพันธ์นั้นมีอยู่ด้วยกันหลายวิธี ซึ่งแต่ละวิธีจะมีค่าคลาดเคลื่อนมากน้อยแตกต่างกันไป โดยคราวนี้จะพูดถึงวิธีการหาปริพันธ์ต่างๆ ดังนี้
วิธีสี่เหลี่ยมคางหมู (Trapzoid Rule)
สำหรับวิธีสี่เหลี่ยมคางหมูนั้น พบว่ามีใช้กันมายาวนาน ตั้งแต่ยุค 50 BC (~พ.ศ. 500) โดยชาวบาบิโลนได้ใช้ในการอินทิเกรตเพื่อหาความเร็วในการเคลื่อนที่ของดาวพฤหัส (อ้างอิง) โดยวิธีนี้จะใช้วิธีการสร้างสี่เหลี่ยมคางหมูขึ้นมาใต้กราฟ เมื่อให้ h เป็นความกว้างของฐานสี่เหลี่ยมคางหมู a คือขอบซ้ายของขอบเขตที่เราต้องการอินทิเกรต และ b คือขอบขวาที่เราต้องการอินทิเกรต โดยเราจะอินทิเกรต 
บนช่วง 0.5 ถึง 1 ได้ดังภาพ
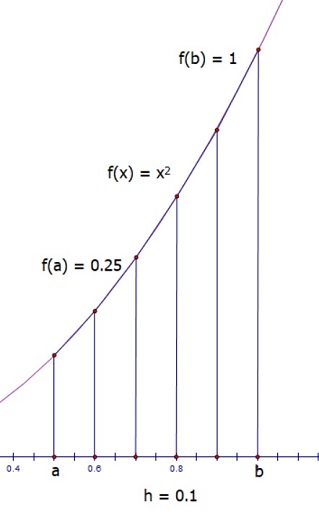
โดยจากสูตรการหาพื้นที่สี่เหลี่ยมคางหมู ได้ว่าพื้นที่ของสี่เหลี่ยมคางหมูด้านซ้ายสุดคือ
เมื่อนำสี่เหลี่ยมคางหมูที่อยู่ในพื้นที่ต้องการอินทิเกรตมาบวกกันจะได้ว่า
จะสังเกตได้ทุกตัวที่ไม่ใช่ตำแหน่งที่ x = a และ x = b จะถูกใช้ซ้ำสองครั้ง จึงสามารถจัดรูปได้เป็น
นั่นคือเราสามารถประมาณค่าอินทิเกรตในช่วยได้โดยวิธีสี่เหลียมคางหมูดังนี้
ซึ่งสามารถเขียนเป็นโค้ดภาษาซีหาอินทิเกรตของ บนช่วง 0.5 ถึง 1 โดยให้ช่วง h กว้าง 0.01 ได้ว่า
จากโค้ดจะได้ผลลัพธ์ว่า Trapzoid = 0.281874 และส่วนค่าจริงนั่นได้ว่า Exact = 0.291667 ซึ่งจะเห็นว่าค่าที่ได้นั้นใกล้เคียงกับผลลัพธ์ของการอินทิเกรตจริงหมูนั้นจะมีค่าคลาดเคลื่อนอยู่ ซึ่งเราสามารถคำนวณค่าคลาดเคลื่อนได้จาก
วิธีซิมสัน (Simpson’s rule)
สำหรับวิธีการอินทิเกรตของซิมสันนั้นจะมีความคลาดเคลื่อนน้อยกว่าวิธีการของสี่เหลี่ยมคางหมู สำหรับที่มานั้น ผมคงต้องไปเรียนในระดับที่สูงขึ้น แต่สำหรับวิธีการนำไปใช้สามารถหาค่าประมาณอินทิเกรตได้จาก
สามารถเขียนเป็นโค้ดภาษาซีหาอินทิเกรตของ บนช่วง 0.5 ถึง 1 โดยให้ช่วง n = 100 ได้ดังนี้
จากโค้ดจะได้ผลลัพธ์ว่า Trapzoid = 0.291667 และส่วนค่าจริงนั่นได้ว่า Exact = 0.291667 ซึ่งจะเห็นว่าค่าที่ได้นั้นใกล้เคียงกับผลลัพธ์ของการอินทิเกรตมาก แต่การอินทิเกรตโดยใช้วิธีซิมสันั้นจะมีค่าคลาดเคลื่อนอยู่ ซึ่งเราสามารถคำนวณค่าคลาดเคลื่อนได้จาก
วิธีการอื่นๆ เพิ่มเติม
นอกจากสองวิธีที่ได้กล่าวถึงขั้นต้นแล้ว ยังมีวิธีการอินทิเกรตแบบอื่นๆ ที่ทำให้ค่าคลาดเคลื่อนน้อยลงได้อีก แต่ก็จะทำให้การเขียนยากขึ้นเช่นกัน หากท่านสนใจสามารถหาอ่านเพิ่มเติมได้ดังนี้